Addition and subtraction of matrices
Requirement: Matrices must be of the same order.
How to: Corresponding elements are added (in addition) or subtracted (in subtraction).
Example
Consider the two matrices given below.


a. Calculate the matrix A + B.
The two matrices are of the same order, (2 × 3), so they can be added.
b. Calculate the matrix A − B.
The two matrices are of the same order, (2 × 3), so they can be subtracted.

Multiplying a matrix by a scalar
A scalar is any real number.
When multiplying a matrix by a scalar, each element of the matrix is multiplied by the scalar.
Example
Calculate the matrix 2A.

Multiplying matrices
Requirement: Matrices can be multiplied if the number of columns in the first matrix is equal to the number of rows in the second matrix.
Example
The order of matrix M is (a × b), where a and b are positive integers.
The order of matrix N is (b × c), where b and c are positive integers.
The product MN is defined because the number of columns in matrix M is equal to the number of rows in the matrix N.
(a × b)(b × c)
The order of the product matrix is (a × c).
The product MN is not always equal to the product NM.
How to: This can be easily explained using an example.
Example
Consider the two matrices given below.

|
and |

|
The order of the matrix M is (2 × 3), where a and b are positive integers.
The order of the matrix N is (3 × 2), where b and c are positive integers.
The product MN is defined because the number of columns in matrix M is equal to the number of rows in the matrix N.
(2 × 3) (3 × 2)
The order of the product matrix is (2 × 2).
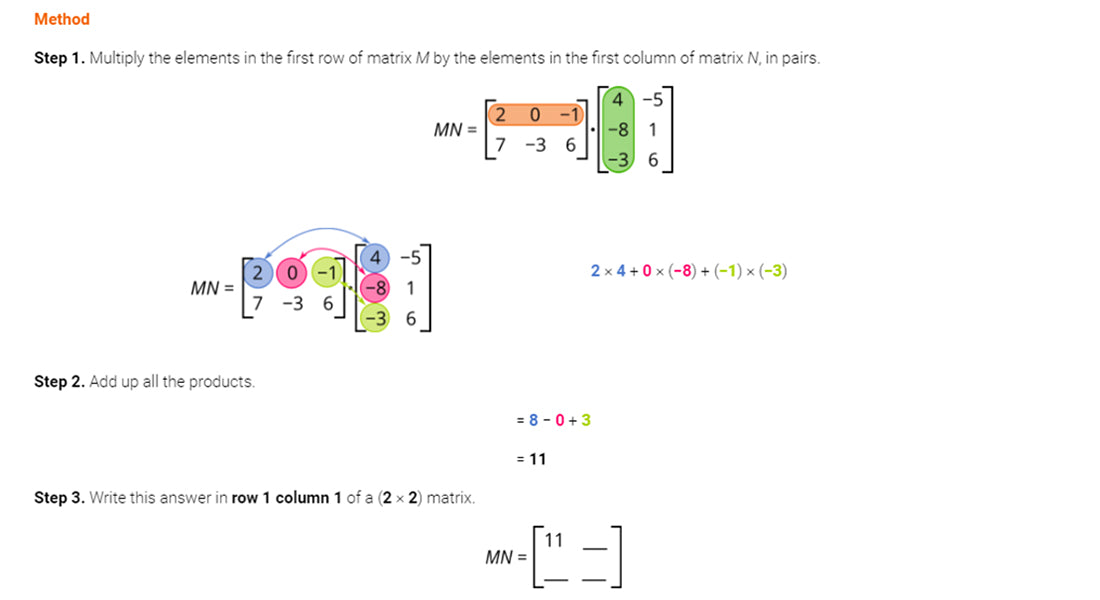
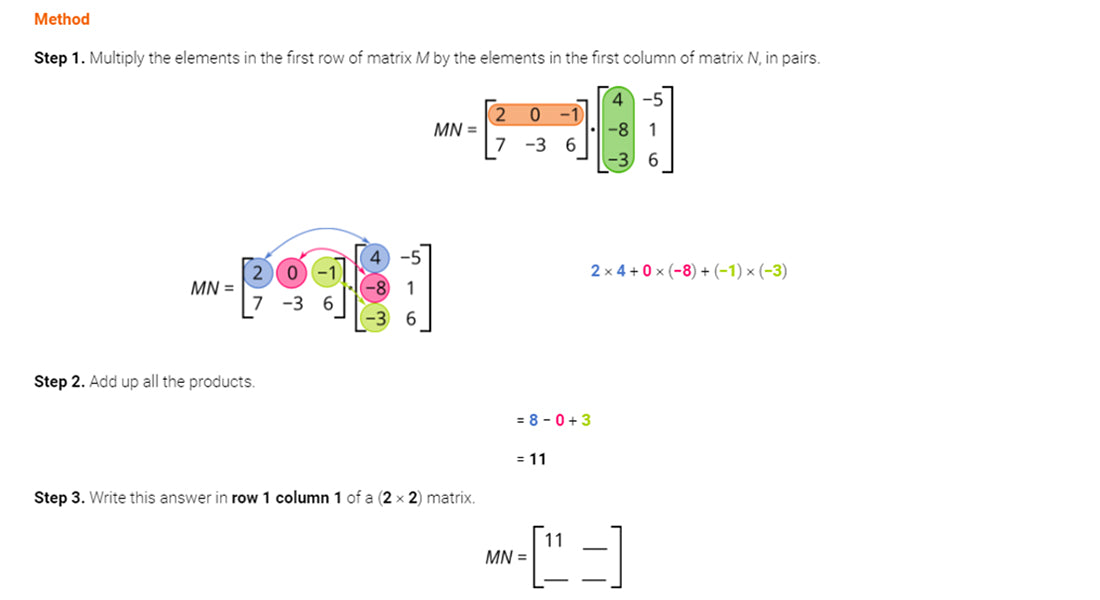
Method
Step 1. Multiply the elements in the first row of matrix M by the elements in the first column of matrix N, in pairs.


|
2 × 4 + 0 × (−8) + (−1) × (−3) |
Step 2. Add up all the products.
= 8 − 0 + 3
= 11
Step 3. Write this answer in row 1 column 1 of a (2 × 2) matrix.

Step 4. Repeat Steps 1 − 3 for the multiplication of row 1 and column 2.


|
2 × (−5) + 0 × 1 + (−1) × 6 = −10 + 0 + (−6) = − 16 |
Step 5. Write this answer in row 1 column 2 in the (2 × 2) matrix.

Step 6. Repeat Steps 1 − 3 for the multiplication of row 2 and column 1.


|
7 × 4 + (−3) × (−8) + 6 × (−3) = 28 + 24 + (−18) = 34 |
Step 7. Write this answer in row 2 column 1 in the (2 × 2) matrix.

Step 8. Repeat Steps 1 − 3 for the multiplication of row 2 and column 2.


|
7 × (−5) + (−3) × 1 + 6 × 6 = (−35) + (−3) + 36 = −2 |
Step 9. Write this answer in row 2 column 2 in the (2 × 2) matrix.